Récursivité
Table des matières
1. Fonctions récursives
1.1. Fonction factorielle
La factorielle d'un nombre peut être définie par récurrence : $$\begin{cases} 0! = 1 \\ \forall n\in\N^*,\, n! = n \times (n-1)! \end{cases}.$$
En Python, une fonction peut s'appeler elle-même. Une telle fonction est dit récursive. L'extrait de gauche suivant définit une fonction fact qui calcule la factorielle d'un entier en argument.
# Version récursive def fact(n): if n == 0: return 1 # 0! = 1 else: return n * fact(n-1) # appel récursif
# Version itérative def fact(n): s = 1 for i in range(1,n+1): s = s * i return s
Écrire une fonction récursive qui prend en argument $n\in\N$ et renvoie $S_n = \sum_{k=1}^n k^4$. On a $S_0 = 0$.
Écrire une fonction u qui renvoie le $n$-ième terme de la suite définie par $u_1 = 1$ et $\forall n\in\N^*,\, u_{n+1} = \frac{u_n}{1+u_n}$.
Écrire deux fonctions récursives qui prennent en argument un entier $n\geq 1$ et affichent les figures suivantes.
On rappelle que l'instruction print("*" * n) affiche une ligne de $n$ caractères "*".
In [1]: triangle1(5) ***** **** *** ** *
In [1]: triangle2(5) * ** *** **** *****
Écrire une fonction liste qui prend en argument un entier $n$, et renvoie une liste comme celle-ci.
assert(liste(4) == [1 , 2 , 1 , 3 , 1 , 2 , 1 , 4 , 1 , 2 , 1 , 3 , 1 , 2 , 1])
1.2. Des fonctions récursives
Décrire ce que fait chacune des fonctions suivantes.
def mystere1(n): assert(n >= 0) if n == 0: return True elif n == 1: return False else: return mystere1(n-2)
def mystere2(a, b): assert(a >= 0) assert(b >= 0) if b == 0: return a else: return mystere2(a+1, b-1)
def mystere3(x, n): assert(n >= 0) assert(x >= 0) if n == 0: return 1 else: return x * mystere3(x, n-1)
def mystere4(a): assert(a >= 0) if a == 0: return 0 r = a % 10 q = a // 10 return r + mystere4(q)
1.3. Le problème de l'arrêt
Pour vérifier la terminaison d'une fonction récursive, il faut vérifier que n'importe quel appel finit par se ramener à un des «cas de base», sans quoi la fonction ne s'arrêtera pas. En pratique, la terminaison est justifiée par le fait que la fonction soit appelée avec des arguments entiers positifs strictement décroissants.
- Expliquer pourquoi la fonction
fci-contre n'est pas correcte. - Comment la modifier pour que l'appel
f(n)renvoie $\lfloor \frac{n}{2}\rfloor$ pour tout entier naturel $n$ ? et $\lfloor \frac{n+1}{2}\rfloor$ ?
def f(n): if n == 0: # Cas de base return 0 # sans appel récursif else: # appel récursif return 1 + f(n-2)
Les fonctions suivantes s'arrêtent-elles pour n'importe quelle valeur de $\N$ de la variable $n$ ? Justifier brièvement en explicitant un cycle infini d'appels s'il en existe un.
def g1(n): if n == 0: return 0 else: m = n // 2 return 1 + g1(m)
def g2(n): if n == 0: return 1 if n % 2 == 0: return 1+g2(n//2) else: return g2(n + 1)
def g3(n): if n == 0: return 1 if n == 1: return 1 m = n // 2 return 1 + g3(m + 1)
def g4(n): # βigstarβigstar if n == 0: return 1 if n % 2 == 0: return g4(n //2 ) else: return g4(3*n+1)
1.4. Pile de récursion et suite de Fibonacci
1.4.1. Pile de récursion
On considère la fonction f suivante.
def f(n): if n == 0: return 0 else: return 1 + f(n-1)
Pour calculer f(3), la machine virtuelle procède comme décrit à droite.
Pour cela, elle doit garder en mémoire tous les appels récursifs en cours, dans ce qu'on appelle la pile de récursion.
La taille de cette pile est limitée (à 1000 par défaut) ; il y a donc une limite à la profondeur des appels récursifs.
En pratique, l'appel f(10000) échoue avec l'erreur RecursionError: maximum recursion depth exceeded in comparison.
- elle rentre dans l'appel f(3)
- elle appelle f(2)
- elle rentre dans l'appel f(2)
- elle appelle f(1)
- elle rentre dans l'appel f(1)
- elle appelle f(0)
- elle rentre dans l'appel f(0)
- elle renvoie 0
- l'appel f(1) renvoie 1 + 0 = 1
- l'appel f(2) renvoie 1 + 1 = 2
- l'appel f(3) renvoie 1 + 2 = 3
1.4.2. Suite de Fibonacci : explosion des appels récursifs
La suite de Fibonacci $(F_n)_{n\in\N}$ est définie par $F_0 = 1$, $F_1 = 1$ et la relation de récurrence double $\forall n\in\N,\, F_{n+2} = F_{n+1} + F_n$.
- Écrire une fonction récursive
fib_recqui calcule $F_n$. - Écrire une version non récursive
fibqui calcule $F_n$, avec une complexité linéaire.
On note $T_n$ le nombre total d'appels récursifs que réalise l'appel fib_rec(n). Cette suite vérifie
$$T_0 = 0,\,T_1 = 0,\,T_2 = 2 \quad\et\quad \forall n\geq 2,\quad T_{n} = 2 + T_{n-1} + T_{n-2}.$$
Montrer qu'il existe $\a\gt 0$ tel que $T_n \underset{n\ra +\i}{\sim} \a \phi^n$, où $\phi = \frac{1 + \sqrt{5}}{2}$. 1
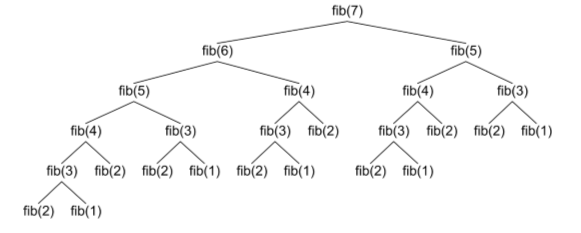
- La version récursive de la fonction
fibest plus simple à écrire, mais elle a une complexité exponentielle. - Ici, le problème n'est pas la profondeur de la pile, qui est de l'ordre de $n$, mais l'explosion du nombre d'appels récursifs.
1.4.3. Mémoïsation ★
La mémoïsation résout le problème de l'explosion des appels récursifs, en gardant en mémoire les valeurs qui ont déjà été calculées, dans une liste, ou un dictionnaire.
l = [1,1] # l[0] = F₀, l[1] = F₁ def mem_fibo_rec(n): if len(l)>n: return l[n] e = mem_fibo_rec(n-2) + mem_fibo_rec(n-1) # après l'appel fibo(n-1), la liste l contient # toutes les valeurs de la suite jusqu'a Fₙ₋₁ assert(len(l) == n) l.append(e) # l[n] = Fₙ return e
# Version avec un dictionnaire # Plus générale d = {0: 1, 1: 1} def mem_fibo_rec(n): if n in d: return d[n] e = mem_fibo_rec(n-2) + mem_fibo_rec(n-1) d[n] = e return e
La complexité de ces deux variantes est linéaire en $n$, comme la version itérative, mais elles utilisent une liste ou un dictionnaire de taille $n$, donc consomment plus de mémoire. On dit que leur complexité spatiale est linéaire.
2. Algorithmes récursifs classiques
2.1. Exponentiation rapide
Écrire une fonction récursive puiss_naive qui prend en argument un flottant x et un entier naturel n et qui renvoie $x^n$.
On utilisera la propriété $\forall n\in\N,\, x^{n+1} = x \times x^n$.
En utilisant les propriétés
- $x^{2p} = x^p \times x^p$
- $x^{2p+1} = x \times x^p \times x^p$
écrire une variante
puissance_rapidede la fonction précédente, pour des exposants $n\geq 0$.- Si $n = 2^m$, combien de produits est-ce que l'appel
puissance_rapide(x, n)réalise ? Justifier brièvement.
Dans le cas général, le nombre d'appels récursifs est d'au plus $\log_2(n)$, donc le nombre de produits réalisés est en $O(\log_2(n))$.
2.2. Algorithme d'Euclide
On s'intéresse au calcul du plus grand diviseur commun (PGCD) de deux entiers naturels $a$ et $b$ qui ne sont pas tous les deux nuls par l'algorithme d'Euclide, en effectuant des divisions euclidiennes successives :
- On effectue la division euclidienne de $a$ par $b$, qui s'écrit $a = bq + r$, avec $r\in\db{0,b-1}$.
- On recommence avec les entiers $b$ et $r$ : on écrit la division euclidienne de $b$ par $r$.
- On s'arrête quand une des divisions euclidiennes donne $0$. Le pgcd de $a$ et $b$ est alors le dernier reste non nul trouvé.
La correction de l'algorithme repose sur les propriétés suivantes.
- Si $b=0$, $\op{pgcd}(a,b) = a$
- Si $a\geq b$, $b\neq 0$, et $a = bq + r$, alors $\op{pgcd}(a,b) = \op{pgcd}(b,r)$.
Écrire une fonction pgcd_rec récursive qui calcule le pgcd de deux entiers naturels en argument.
Algorithme d'Euclide étendu
Dans le calcul du pgcd de $a,b$ par l'algorithme d'Euclide, notons $a_n, b_n$ les entiers considérés à l'issue de la $n$-ième itération de la boucle, définis par $$\begin{cases}a_0 = a \\ b_0 = b \end{cases}\quad \et \quad \forall n\in\N,\,\begin{cases}a_{n+1} = b_n \\ b_{n+1} = r_n \end{cases}, \text{ où } a_n = b_n q_n + r_n \text{ est la division euclidienne.}$$
On se convainc aisément que pour tout $n\in\N$, $a_n$ et $b_n$ sont des combinaisons linéaires entières des entiers $a,b$ d'origine, c'est-à-dire qu'il existe $u_n,v_n\in\Z$ tels que $b_n = u_n a + v_n b$. En particulier, à la dernière étape, $\op{pgcd}(a,b)$ est lui-même une combinaison linéaire de $a,b$ :
Soient $a,b\in\N$. Il existe un couple $(u,v)\in\Z^2$ tel que $\quad \op{pgcd}(a,b) = au + bv$.
L'ensemble $\{au + bv,\, u,v\in\Z\}$ est l'ensemble des multiples de $\op{pgcd}(a,b)$.
- Écrire une fonction récursive
eucl_etenduqui prend en argument deux entiers $a,b\in\N$ et renvoie un couple de Bézout de $a,b$, c'est-à-dire un couple d'entiers relatifs $(u,v)$ tel que $au + bv = \op{pgcd}(a,b)$. - En déduire une fonction
inversequi prend en argument $a, b$ et renvoie un inverse de $a$ modulo $b$ s'il en existe un, ouNonesinon.
2.3. Recherche dichotomique récursive
- Expliquer pourquoi l'implémentation
mauvaise_rech_dichon'est pas efficace. - Compléter l'implémentation
rech_dicho, qui utilise une fonction auxiliaire récursive.
def mauvaise_rech_dicho(t, e): n = len(t) if n == 0: return False if n == 1: return t[0] == e m, c = n // 2, t[n // 2] if e > c: return mauvaise_rech_dicho(t[m+1:],e) if e < c: return mauvaise_rech_dicho(t[:m],e) return True
def rech_dicho(t, e): # Fonction auxiliaire récursive, qui renvoie True ssi # e est présent, entre les indices a inclus et b exclu. def rech_aux(a, b): … # On peut faire référence à t et e ici. # La fonction rech_dicho se contente d'appeler rech_aux return rech_aux(0, len(t))
2.4. Tri fusion
Pour trier une liste, l'algorithme de tri fusion consiste en les étapes suivantes.
- On découpe la liste en deux listes de tailles égales (à peu près).
- Par des appels récursifs, on trie chacune des deux listes.
- On fusionne les deux listes triées, en une seule liste triée.
- Écrire une fonction
decoupequi prend en argument une listelet renvoie un couple de listesl1etl2telles quelen(l1) == len(l2)oulen(l1) == len(l2) - 1. - Écrire une fonction
fusionqui prend en argument deux listesl1etl2triées et qui renvoie une nouvelle liste triée, contenant tous les éléments del1et del2. 2 - Écrire une fonction récursive
tri_fusion. Celle-ci renverra une nouvelle liste.
Analyse de la complexité temporelle
On note $F_n$ le nombre d'opérations effectuées, dans le pire des cas, par un appel tri_fusion sur une liste de longueur $n$. On suppose que la suite $(F_n)_{n\in\N}$ est croissante3.
Lors de l'appel tri_fusion(n) on
- découpe la liste en deux listes, de tailles $\lfloor \frac{n}{2}\rfloor$ et $\lceil \frac{n}{2} \rceil$
- appelle
tri_fusionsur les deux listes obtenues - fusionne les deux listes triées
Les étapes 1. et 3. ont une complexité linéaire. L'étape 2. réalise au plus $F_{\lfloor \frac{n}{2}\rfloor} + F_{\lceil \frac{n}{2} \rceil}$ opérations. On en déduit qu'il existe $C\in\R_+$ tel que $\quad\displaystyle\forall n\geq 2,\, F_n \leq Cn + F_{\lfloor \frac{n}{2}\rfloor} + F_{\lceil \frac{n}{2} \rceil}$.
Pour simplifier l'étude, on suppose dans un premier temps que $n = 2^p$. On a alors $\forall p,\,F_{2^p} \leq C 2^p + 2F_{2^{p-1}}$. En réutilisant successivement cette même inégalité, on obtient $$\begin{aligned}F_{2^p} & \leq C 2^p + 2F_{2^{p-1}} \leq C2^p + 2(C 2^{p-1} + 2 F_{2^{p-2}}) = C 2^p + C 2^p + 4 F_{p-2} \\ & \leq C 2^p + C 2^p + C 2^p + 2^3 F_{p-3} \\ & \leq \, \dots \\ & \leq p C 2^p + 2^p F_1 = C p 2^p\end{aligned}$$
Pour $n$ quelconque, on pose $p = \lfloor \log_2(n)\rfloor + 1$, de sorte que $n\lt 2^p$ et $2^p \leq 2n$. On a $$F_n \leq F_{2^p} \leq C p 2^p \leq 2C(\log_2 (n) + 1)n \leq C' n \ln n.$$
L'algorithme de tri fusion a une complexité en $O(n\ln n)$ dans le pire des cas, où $n$ est la longueur de la liste.
Optimalité de la complexité ★
On s'intéresse à des algorithmes de tri dont la logique n'utilise que des comparaisons entre les éléments permettant de trier toutes les permutations de la liste l = [1, 2, …, n]. Pour toute permutation $\sigma$, on note $N_{\sigma}$ le nombre de comparaisons utilisées par l'algorithme pour trier cette permutation. On note $N = \max_{\sigma}(N_{\sigma})$ le nombre de comparaisons dans le pire des cas.
On a $N \geq \log_2 (n!)$.
Il y a $n!$ permutations de l, et les réalisations de l'algorithme sur chaque permutation doivent être différentes. Il y a au plus $2^N$ réalisations de l'algorithme, donc $2^N\leq n!$, c'est-à-dire $N\leq \log_2 (n!)$.
$\log_2(n!) = \frac{\ln (n!)}{\ln 2} \sim \frac{n \ln n}{\ln 2}$.
On a $\frac{1}{n!}\sum_{\sigma} N_{\sigma}\geq \log_2 (n!) - 3$.
Pour chaque $\sigma\in\mc S_n$, on note $N_{\sigma}$ le nombre de comparaisons de l'algorithme pour la permutation $\sigma$.
On doit avoir, pour tout $k$, $\big|\{\sigma \mid N_{\sigma} \leq k\}\big|\leq 2^k$, donc $\big|\{\sigma \mid N_{\sigma} \geq k\}\big|\geq n! - 2^{k-1}$. Alors $$\sum_{\sigma} N_{\sigma} = \sum_{k = 1}^{\i}\sum_{\sigma \mid N_{\sigma} = k} k = \sum_{k = 1}^{+\i} \sum_{\sigma \mid N_{\sigma}\geq k} 1 \geq \sum_{k =1 }^{2^{k-1} \leq n!} (n! - 2^{k-1}) = \big(\lfloor \log_2(n!)\rfloor + 1\big) n! - \big(2^{\lfloor \log_2(n!)\rfloor + 1} - 1\big)\geq (\log_2(n!) - 3)n!$$
Complexité spatiale ★
Malgré sa complexité temporelle en $O(n\ln n)$, la version implémentée dans l'exercice 2.4 est lente, à cause du grand nombre de copies de listes réalisées (chaque appel l[i:j] réalise une copie).
Bien que ces copies ne changent pas l'ordre de grandeur du nombre d'opérations total, elles changent l'ordre de grandeur de la quantité de mémoire utilisée. On pourrait justifier que la quantité de mémoire totale utilisée (on parle de complexité spatiale) est de l'ordre de $O(n\ln n)$, alors qu'un algorithme optimal n'en utilise que $O(n)$.
Ce défaut n'est pas intrinsèque au tri fusion, uniquement à cette implémentation en Python. Voici une autre implémentation du tri fusion qui n'alloue que $O(n)$ cases mémoires supplémentaires. Autre différence : au lieu de renvoyer une nouvelle liste triée, elle modifie la liste donnée en argument.
def fusion(l): # liste tampon t = [0] * len(l) # On définit une fonction auxiliaire, qui prend # en argument deux entiers a, b et qui va trier # la liste, entre les indices a (inclus) et b # (exclu) def fusion_aux(a, b): # Pour un seul élément, il n'y a rien à # faire if b - a <= 1: return c = (a + b) // 2 # On trie les deux moitiés fusion_aux(a, c) fusion_aux(c, b) # On fusionne les deux moitiés dans le # tampon (de a à b)
i, j = 0, 0 while i < (c-a) and j < (b-c): if l[a+i] <= l[c+j]: t[a+i+j] = l[a+i] i += 1 else: t[a+i+j] = l[c+j] j += 1 if i == c-a: for k in range(j, b-c): t[a+i+k] = l[c+k] else: for k in range(i, c-a): t[a+k+j] = l[a+k] # On recopie la liste t dans l for k in range(a,b): l[k] = t[k] # Appel de la fonction auxiliaire fusion_aux(0, len(l))
2.5. Tri pivot
Pour trier une liste, l'algorithme de tri par pivot consiste en les étapes suivantes.
- On choisit un élément de la liste, (en pratique, son premier élément), qui va jouer le rôle de pivot.
- On modifie la liste de sorte que tous les éléments inférieurs ou égaux au pivot soient à sa gauche, et les autres éléments soient à sa droite. En particulier, le pivot est à sa place finale, une fois la liste triée.
- Par des appels récursifs, on trie chacune des deux sous-listes, à droite et à gauche du pivot.
Cet algorithme modifiera la liste sur place plutôt que d'en créer une nouvelle.
Implémenter ce tri. On utilisera une fonction auxiliaire tri_pivot_aux qui prend en argument deux entiers a,b et qui se charge de trier la sous-liste de la liste d'origine l entre les indices a (inclus) et b (exclu).
def tri_pivot(l): # Définition d'une fonction auxiliaire, à l'intérieur de # tri_pivot. L'appel tri_pivot_aux(a, b) doit trier la liste # l entre les indices a et b def tri_pivot_aux(a, b): ... tri_pivot_aux(0, len(l))
Complexité du tri pivot
L'algorithme est d'autant plus rapide que les pivots successifs partitionnent la liste en deux parties de tailles égales. Dans le meilleur des cas, si le pivot est une médiane à chaque étape, la complexité vérifie la même relation de récurrence que le tri fusion : $F_n = F_{\lfloor \frac{n}{2}\rfloor} + F_{\lceil \frac{n}{2} \rceil} + Cn$, qui donnerait une complexité en $O(n\ln n)$.
Dans le pire des cas, si tous les pivots choisis sont des extremums de la liste, on obtient une relation de récurrence en $F_n = Cn + F_{n-1}$, qui donne $F_n = Cn + C (n-1) + \dots + C = C \frac{n(n+1)}{2}$, donc une complexité quadratique.
C'est le cas si la liste en entrée est déjà triée, par ordre croissant ou décroissant.
«En moyenne», le tri pivot a une complexité en $O(n\ln n)$.
Malgré sa complexité quadratique dans le pire des cas, le tri pivot est en pratique plus rapide que le tri fusion (entre autres parce qu'il n'alloue pas de mémoire supplémentaire). Il est parfois appelé tri rapide, et quicksort en anglais.
Il est possible (mais très technique) de modifier l'algorithme pour choisir le pivot de manière plus intelligente, de sorte à garantir une complexité en $O(n\ln n)$ dans le pire des cas.
2.6. Parcours en profondeur récursif d'un arbre ★
On considère un arbre, dont les sommets sont les entiers de $0$ à $n-1$, et dont la racine est le sommet $0$.
On représente cet arbre par une liste enfants de taille $n$, où enfants[i] est la liste des enfants du sommet $i$.
À partir de la racine, on veut parcourir cet arbre en profondeur, et appeler une fonction f donnée à chaque sommet de l'arbre, dans l'ordre du parcours.
Un parcours en profondeur (de gauche à droite) est un parcours dans lequel si un sommet à plusieurs enfants $e_1,\dots, e_m$, on visite d'abord tous les descendants de $e_1$, puis tous les descendants de $e_2$, etc.
Parmi les parcours en profondeurs, on distingue
- le parcours préfixe, où l'on appelle la fonction
fsur un sommet $s$ avant de l'appeler sur ses descendants. - le parcours infixe, où l'on appelle la fonction
faprès l'avoir appelé sur ses descendants.
Implémenter deux fonctions parcours_prefixe et parcours_infixe qui prennent en argument la liste enfants et une fonction f et réalisent les parcours décrits.
3. Exercices
Écrire une fonction récursive decomp qui prend en argument un entier $n\in\N^*$ et renvoie l'unique paire d'entiers $(p, m)$ avec $p\in\N$ et $m\in\N^*$ impair telle que $n = 2^p m$. Par exemple, l'entier $12$ s'écrit comme $12 = 4\times 3 = 2^2 \times 3$.
Essayez : decomp
Écrire une fonction récursive
somme_chiffresqui calcule la somme des chiffres décimaux d'un entier naturel.Par exemple,
somme_chiffres(123)renverra $6$.- Écrire une fonction récursive
chiffres_pairsqui prend en argument un entier naturelnet renvoieTruesi tous ses chiffres décimaux sont pairs.
Essayez : somme_chiffreschiffres_pairs
- Écrire trois fonctions
coef_bind'arguments $0\leq p\leq n$ qui renvoient ${n\choose p}$, utilisant respectivement la définition comme quotient de factorielles, la formule de Pascal, et la formule «du capitaine» ${n \choose p} = \frac{n}{p} {n-1 \choose p-1}$. - Discuter de l'efficacité des trois variantes.
On représente une partie de $\db{1,n}$ par la liste de ses éléments, par ordre croissant. On veut écrire une fonction parties qui prend $n$ en argument et renvoie la liste des parties de $\db{1,n}$.
Par convention,
parties(0)renvoie la liste[[]], puisque l'ensemble vide $\emptyset$ admet une unique partie.Que renvoient
parties(1)etparties(2)?Implémenter la fonction
parties, d'une manière récursive.On remarquera qu'il y a deux types de parties de $\db{1,n}$ : celles qui ne contiennent pas $n$, et qui sont donc des parties de $\db{1,n-1}$ et celles qui contiennent $n$.
Essayez : Question 1parties
Alice et Bob jouent au jeu suivant : $n$ bâtonnets sont alignés. Tour à tour, les joueurs doivent retirer un, deux ou trois bâtonnets. Le joueur qui ne peut pas retirer de bâtonnet (s'il n'y en a plus) perd.
Si $n=1,2,3$, le premier joueur a une stratégie gagnante (laquelle ?). Quel que soit $n$, un des deux joueurs a une stratégie gagnante.
Écrire une fonction est_gagnant qui prend en argument un entier n et qui renvoie True si le premier joueur a une stratégie gagnante, et False sinon.
On peut décrire simplement la stratégie gagnante, mais ce n'est pas l'objectif ici.
Essayez : est_gagnant
Écrire une fonction chaine_extraite qui prend en argument deux chaînes c1 et c2 et qui renvoie True si la chaîne c2 peut être obtenue à partir de la chaîne c1 en retirant certains caractères.
assert(chaine_extraite("aabbcc", "abc"))assert(not(chaine_extraite("ababc", "baba")))
Une permutation de $\db{1,n}$ est une liste de taille $n$ contenant tous les entiers de $1$ à $n$.
- Écrire une fonction
permutationsqui renvoie la liste de toutes les permutations de $\db{1,n}$. - Combien y a-t-il de permutations de $\db{1,n}$ ?
Dans le jeu des tours de Hanoï, $n$ disques de largeurs $1,2,\dots, n$ sont initialement empilés sur une tour, du plus large au moins large. Deux autres tours, vides, sont disponibles. À chaque étape, on peut déplacer un disque, situé en haut d'une des tours sur une autre tour, mais un disque ne peut être posé que sur un disque plus large. Le but du jeu est de déplacer toute la tour initiale sur la troisième tour.

- Décrire une stratégie récursive.
- Écrire une fonction
tour_hanoiqui prend en argument un entier $n$ et qui résout le problème, en imprimant une liste d'instructions de la forme «On déplace le disque de largeur $\dots$ de la tour $\dots$ à la tour $\dots$».
Notes de bas de page:
Vérifier que la suite $V_n = T_n + 2$ satisfait une équation de récurrence linéaire d'ordre $2$.
On ajoutera petit à petit des éléments dans la nouvelle liste, en progressant alternativement dans l1 ou l2. On utilisera deux variables intermédiaires i1 et i2 représentant les indices où on en est dans l1 et l2.
Si elle ne l'était pas, il faudrait remplacer les $F_n$, par $G_n = \max\limits_{1\leq k\leq n} F_k$. La suite $(G_n)$ est forcément croissante et vérifie la même inéquation de récurrence.